Magnetic force is a fundamental interaction in physics that governs the behavior of charged particles and magnetic materials. It’s the force that causes magnets to attract or repel each other and influences the motion of charged particles in magnetic fields.
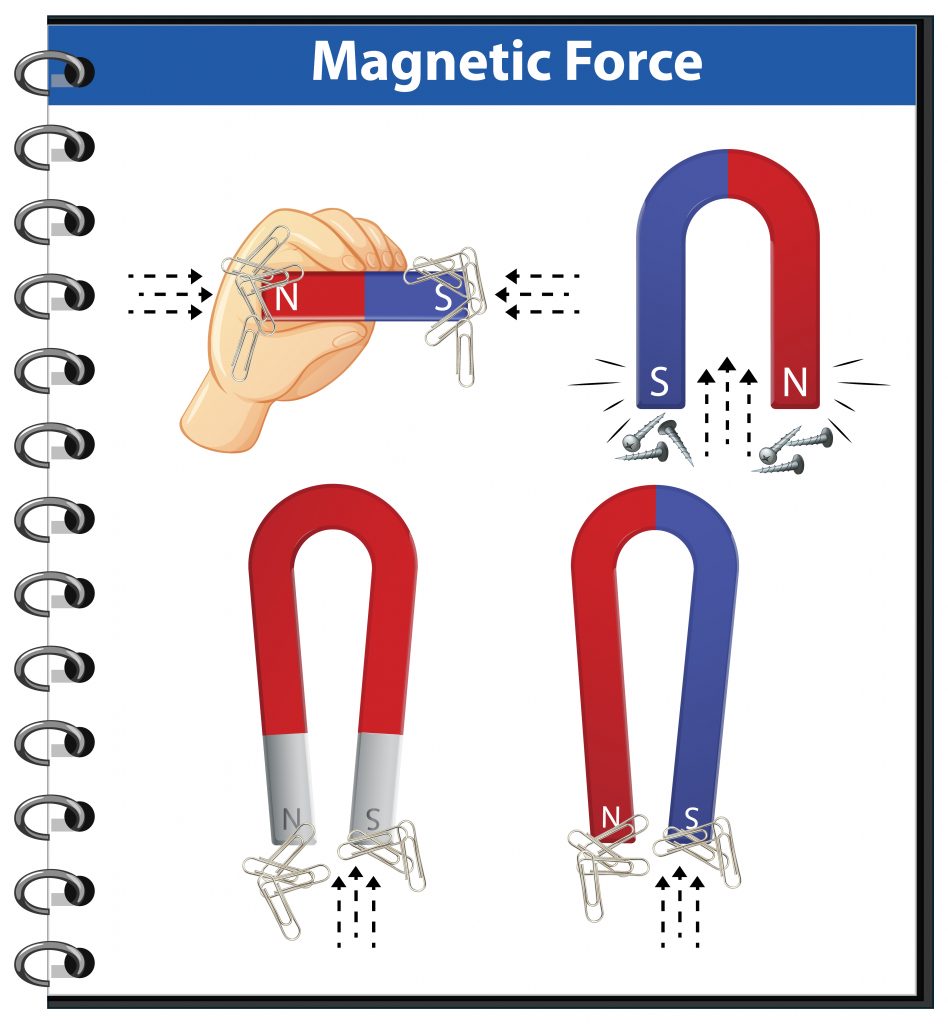
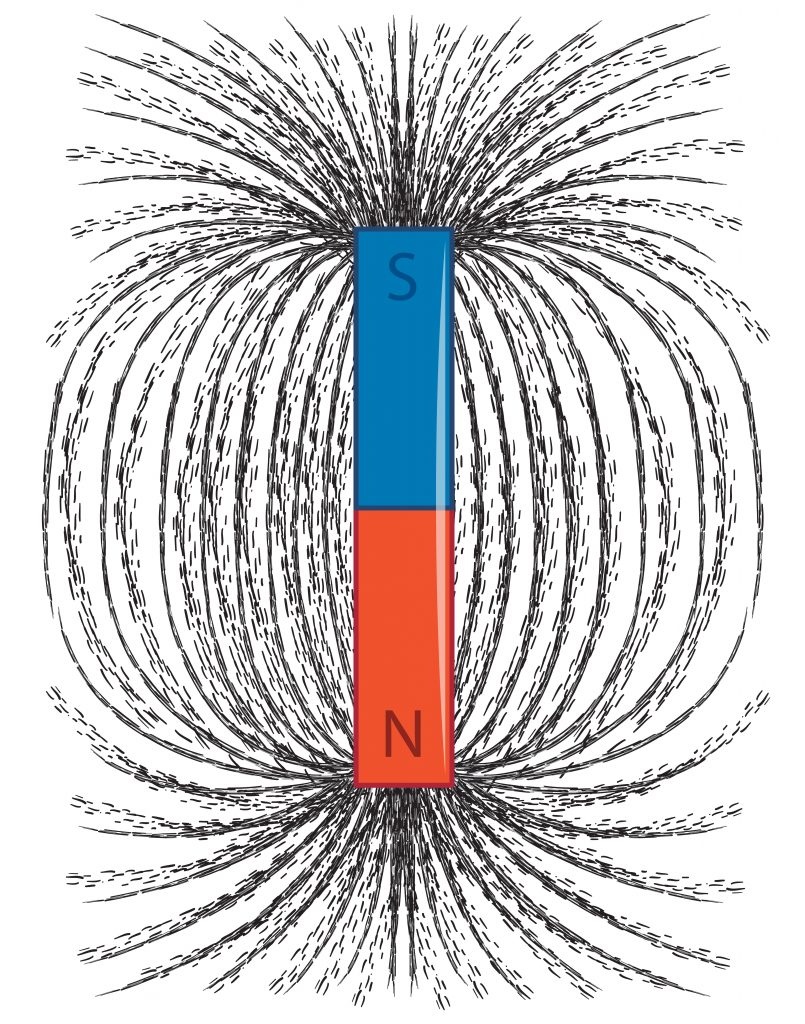
In this article, we’ll explore the concept of magnetic force, its underlying principles, mathematical descriptions, its diverse applications in our daily lives, and the magnetic force of neodymium magnets.
Key Takeaways
- Magnetic Force is a fundamental force that arises from the motion of charged particles and is part of the electromagnetic force.
- The Lorentz Force law describes how electric and magnetic fields interact to influence the motion of charged particles.
- The Right-Hand Rule helps determine the direction of the magnetic force on a moving charge.
- Magnetic Force plays a key role in everyday technologies, such as electric motors, MRI machines, maglev trains, and data storage devices.
- Applications of Magnetic Force extend to various scientific and industrial fields, making it essential for both technological advancements and natural phenomena like Earth’s magnetic field.
- The magnetic force of neodymium magnets.
1. What Is Magnetic Force?
Magnetic force refers to the attraction or repulsion between objects that results from the motion of electric charges. The force is a component of the electromagnetic force, one of the four fundamental forces of nature, and arises due to the motion of charges.
When charged particles move, they generate magnetic fields, and these fields can exert forces on other moving charges. It interplay between electricity and magnetism is encapsulated in the concept of the electromagnetic force.
2. The Lorentz Force: Unifying Electric and Magnetic Forces
The total force experienced by a charged particle moving in both electric and magnetic fields is described by the Lorentz force law:
F=q(E+v×B)
Where:
- F is the total force on the particle.
- q is the charge of the particle.
- E is the electric field.
- v is the velocity of the particle.
- B is the magnetic field.
- × denotes the cross product, indicating that the magnetic force is perpendicular to both the velocity of the particle and the magnetic field.
The equation highlights how electric and magnetic fields interact to influence the motion of charged particles.
3. Magnetic Force on Moving Charges
The magnetic force on a moving charge depends on several factors:
- Charge Magnitude (q): Larger charges experience greater forces.
- Velocity (v): Faster-moving charges experience stronger forces.
- Magnetic Field Strength (B): Stronger magnetic fields exert greater forces.
- Angle Between Velocity and Magnetic Field: The force is maximized when the velocity and magnetic field are perpendicular. If the velocity and magnetic field are parallel or antiparallel, the magnetic force is zero.
The magnitude of the magnetic force can be calculated using:
F=qvBsin(θ)
Where θ is the angle between the velocity vector and the magnetic field vector. The formula underscores that the magnetic force is greatest when the velocity and magnetic field are perpendicular.
4. Direction of Magnetic Force: The Right-Hand Rule
Determining the direction of the magnetic force involves the right-hand rule. For a positive charge moving with velocity v in a magnetic field B:
- Point your fingers in the direction of v.
- Curl them toward B.
- Your thumb points in the direction of the magnetic force F.
For a negative charge, the force direction is opposite to that indicated by your thumb.
5. Magnetic Force on Current-Carrying Wires
Not only moving charges but also current-carrying conductors experience magnetic forces. When a current flows through a wire placed in a magnetic field, the magnetic force acts on the wire, which can lead to motion. The force per unit length on a straight, current-carrying wire in a uniform magnetic field is given by:
LF=IBsin(θ)
Where:
- I is the current.
- B is the magnetic field strength.
- θ is the angle between the magnetic field and the current direction.
The principle is fundamental to the operation of electric motors, where magnetic forces are harnessed to produce rotational motion.
6. Applications of Magnetic Force
Magnetic forces have numerous applications that are integral to modern technology and daily life:
Electric Motors
Electric motors convert electrical energy into mechanical energy using magnetic forces. When current flows through a coil in a magnetic field, the resulting force causes the coil to rotate, driving various mechanical devices.
Magnetic Resonance Imaging (MRI)
MRI scanners utilize strong magnetic fields and magnetic forces to produce detailed images of internal body structures. The magnetic force aligns the spins of atomic nuclei, and radio waves are used to detect changes in this alignment, creating images of tissues and organs.
Mass Spectrometers
Mass spectrometers separate charged particles based on their mass-to-charge ratio using magnetic fields. As ions pass through a magnetic field, they experience a force that causes them to follow curved paths. The radius of curvature depends on their mass-to-charge ratio, allowing for their separation and identification.
Magnetic Levitation (Maglev) Trains
Maglev trains use magnetic forces to levitate above tracks, eliminating friction and allowing for high-speed travel. By manipulating magnetic fields, these trains can be propelled forward smoothly and efficiently.
Data Storage
Hard drives and other data storage devices rely on magnetic forces to read and write data. Magnetic heads manipulate the magnetic properties of disk surfaces to encode and retrieve information.
7. The Magnetic Force of Neodymium Magnets
Neodymium magnets, composed of an alloy of neodymium, iron, and boron (Nd₂Fe₁₄B), are renowned for their exceptional magnetic strength. They are the most powerful type of permanent magnet commercially available, surpassing other magnets like ferrite or alnico in performance.
Neodymium magnets are graded based on their maximum energy product, denoted as (BH)ₘₐₓ, which indicates the density of magnetic energy. Grades typically range from N35 to N52, with higher numbers representing stronger magnets. For instance:
- N35 Grade: Remanence (B_r) of approximately 1.1 Tesla and a coercivity (H_cj) around 750 kA/m.
- N52 Grade: Remanence up to 1.4 Tesla and coercivity near 2000 kA/m.
8. Conclusion
Magnetic force is a fundamental aspect of electromagnetism, influencing a wide range of physical phenomena and technological applications. From the operation of electric motors to the functionality of MRI scanners, magnetic forces play a crucial role in modern life. Understanding these forces enhances our comprehension of both natural processes and the technologies that shape our world.
9. FAQs
What is the difference between electric force and magnetic force?
- Electric Force: Acts between stationary charges; its strength is described by Coulomb’s law.
- Magnetic Force: Acts between moving charges; it depends on the velocity of the charges and the magnetic field.
Can magnetic forces do work?
Yes, magnetic forces can do work when they cause charged particles or current-carrying wires to move, converting magnetic potential energy into kinetic energy.
Why do magnetic forces not do work on stationary charges?
Magnetic forces do no work on stationary charges because work is defined as force applied over a distance. Since stationary charges do not move, no work is done.
How do magnetic fields affect human health?
Exposure to strong magnetic fields, such as those used in MRI machines, is generally considered safe. However, extremely high magnetic fields can pose health risks, and safety guidelines are followed to mitigate potential effects.
Are magnetic forces responsible for Earth’s magnetism?
Yes, Earth’s magnetic field is generated by the motion of molten iron and other metals in its outer core, creating a dynamo effect that produces a global magnetic field.
